1 linii de tensiune

§2.1 linii de tensiune. Curgerea vectorului intensitate.

Câmpul electric este unic determinată dacă amplitudinea (modulul) și vectorul de direcție pentru fiecare punct al spațiului. Acest lucru se poate face, în cazul în spațiul pentru a efectua așa-numita linie de tensiune (linia de alimentare) în câmp electric.

Aceste linii sunt desenate astfel încât tangenta la linia de tensiune coincide cu direcția vectorului

în acest moment, și „densitatea“ liniilor reflectă mărimea vectorului intensitate . Dacă punctul dat în spațiu unde câmpul electric este prezent, adică, plasați o unitate de suprafață, perpendicular pe liniile de forță, numărul de linii care trece prin această zonă, este numeric egal cu magnitudinea tensiunii.

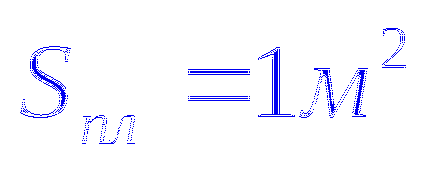
Pentru punctul de taxare liniile de câmp sunt linii radiale. Pentru sarcini pozitive - lăsând în sarcina infinit, pentru negativ - vin la o taxa de la infinit.

H

Aydem numărul total de N. care pleacă / sosesc la / la taxa (y). Pentru punctul de încărcare surround, că suprafața sferică arbitrară de rază r. apoi:

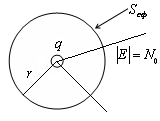
Astfel, numărul de linii N de ieșire din taxa rămâne întotdeauna constantă. și anume

Acest lucru implică faptul că liniile de tensiune oriunde, cu excepția taxei nu începe și se termină: o sarcină pozitivă pentru a merge la infinit, pentru o negativa vine de la infinit și se termină la o taxă. În acest domeniu, liniile nu se intersectează unele cu altele. Această proprietate linii de vector este comun pentru toate câmpurile electrostatice care câmpurile create de sistemul de taxe de staționare.

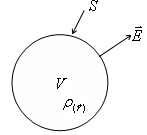
Să considerăm o suprafață care se află în câmpul electric S.

. Distingem acest infinitezimale dS element de suprafata. lăsa - a dS vector unitate normală pentru acest element. Apoi, numărul de linii care străbat această zonă este:

Numărul total de linii (1)

Expresia (1) se numește vectorul de curgere prin suprafața S.

Vector Feed - cantitatea scalară.

Sensul vectorului fluxului E - numărul de linii de forță care strabat această suprafață S.

E

În cazul în care o suprafață închisă, se obișnuiește să se calculeze fluxul vectorului în afară din zona de prindere. Prin urmare, în condiții normale se înțelege un vector îndreptat spre exterior de la suprafața S.

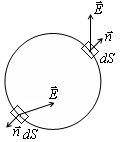
Vectorul de expresie se numește un flux prin suprafața închisă.

§2.2. Teorema Gauss.

În secțiunea precedentă, am stabilit că pentru o taxă punct de curgere prin domeniul de aplicare (suprafață închisă):

În cazul în care suprafața are o „cutelor“, linia de tensiune este întotdeauna traverseze limita suprafețele de un număr impar de ori, și, prin urmare, orice suprafață care înconjoară taxa

În cazul în care există un sistem de taxe, înconjurat arbitrar de suprafață S închisă, pe baza principiului superpoziției poate fi scris:

Expresia (2) se numește teorema lui Gauss: vector de curgere printr-o suprafață oarecare este egală cu suma algebrică a taxelor limitate în interiorul suprafeței împărțită.

În special, în cazul în care nu există nici o taxă în interiorul S, sau;

În cazul în care taxa este distribuită în interiorul suprafeței este continuă cu densitatea în vrac. apoi încărcătura totală în interiorul și fluxul S. (* 2)

T

eorema Gauss în forma (2) și (2 *), se numește teorema lui Gauss în formă integrală.

Teorema lui Gauss poate fi exprimat în formă diferențială. Pentru aceasta folosesc teorema Ostogradskogo-Gaussian, care face legătura între integralei de pe suprafața S închisă cu integrala pe V. Volumul Această suprafață limitată S.

Dacă introduceți un simbol nabla operator de vector:

Și, în sfârșit obținem:

Relația (3) este forma diferențială a teoremei lui Gauss.

Ecuațiile (2) și (* 2), (3) - unul dintre rapoartele Electrostatică de bază. Teorema lui Gauss este valabilă pentru următoarele motive:

Forța de interacțiune dintre sarcini punctiforme este invers proporțională cu pătratul distanței dintre tarifele.

Caracterul central al forțelor de interacțiune.

superpoziție liniară a efectelor datorate diferitelor taxe.

semnificație fizică profundă a teoremei lui Gauss. în natură, există sarcini electrice și sunt sursa câmpului electric.

Așa cum se va arăta mai jos relația (2) (* 2), (3), incluse în așa-numitul Maxwell Ecuații electrodinamicii clasice ca prima ecuație.

§2.3. Aplicarea Legii lui Gauss pentru a găsi câmpul electrostatic.

Pentru încărcările electrostatice cu simetrie sferică și cilindrică, teorema Gauss ne permite să se calculeze domeniul taxei într-un mod mai simplu decât în ​​cazul în care au fost calculate direct din legea lui Coulomb și principiul superpoziției.

a) Domeniul benzii fără sfârșit este încărcată uniform.

Densitatea de încărcare liniară:

P

câmp asschityvaya pe baza legii lui Coulomb, constatăm că , unde a este distanța până la firul.

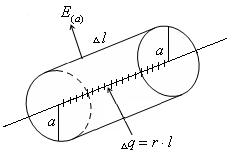
Obținem același rezultat pe baza teoremei Gauss. Evident, tensiunea este perpendiculară pe filament. La o distanță de un filament. Astfel, problema are o simetrie cilindrică în jurul unei axe care coincide cu firul.

Ne înconjoară cilindrul fir de rază și lungime. Deoarece vectorul perpendicular pe suprafața cilindrului, liniile de forță Eprohodyat numai prin suprafața laterală. Aplicând teorema Gauss obținem:

Avem același rezultat.

b

) Domeniul încărcat metalic solid (minge cav).

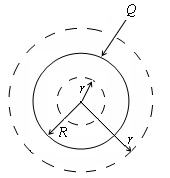
Pune pe minge de metal taxa Q. Taxa este distribuit uniform pe suprafața sferei. În interiorul mingea nu se percep taxe. După ce a descris centrul sferei în jurul sferei cu raza r arbitrar

Astfel, câmpul din interiorul sferei de metal dacă este solid sau gol la interior este absent.

In mod similar, aplicând teorema Gauss pentru puncte din afara sferei (r> R), am găsit:

Câmpul în afara sferei coincide cu domeniul Q. taxa punct situat în centrul sferei.

În apropierea suprafeței (în afara), este de asemenea ușor de determinat dacă E r = R pune în ultima expresie. Apoi, - densitatea de încărcare de pe suprafața sferei. și

Această expresie pentru E este valabil pentru oricare dintre corpul metalic încărcat.

Trebuie remarcat faptul că corpul de metal de orice formă pentru diferite puncte de suprafața corpului.

c) Considerăm acum un plan infinit pe care taxa este distribuită uniform, cu o densitate de suprafață.

Găsim intensitatea E la o distanță arbitrară dintr-un avion. Este ușor de observat că vectorul perpendicular pe planul.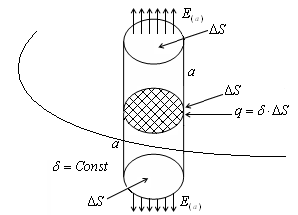

Am ales o zonă arbitrar pe un plan.

Construi pe baza unui cilindru vertical și o înălțime deasupra planului și dedesubt. La capetele cilindrului și este îndreptat din cilindru. Prin urmare, fluxul de vector trece numai prin capetele. Aplicăm teorema lui Gauss:

Astfel, câmpul electric este independent de distanța a la toate punctele de spațiu deasupra și dedesubtul planului de același :. Un astfel de câmp este numit omogen.

g) Să ne determine câmpul electric E în interiorul și este uniform încărcat în volum unei R. rază sferă

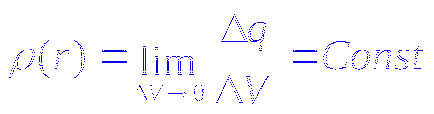
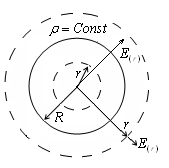
Vom descrie o sferă în jurul centrului sferei cu raza r arbitrar

Folosind teorema lui Gauss:

Dacă r

Astfel, câmpul este încărcat de sfera de volum coincide cu domeniul Q. taxa punct situat în centrul sferei.

W

Dependența modulului vectorului este prezentată în Figura: crește liniar până la suprafața sferei R. și apoi cade quadratically .

d) Câmpul între două planuri paralele, încărcat cu sarcini opuse.

P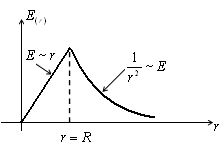

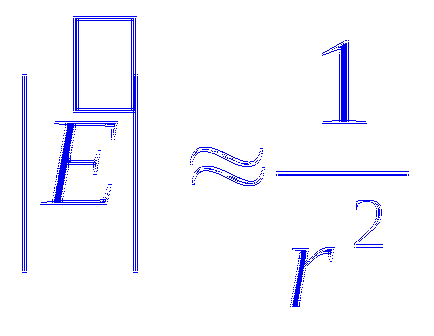
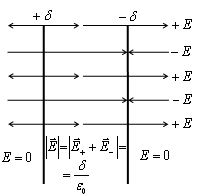
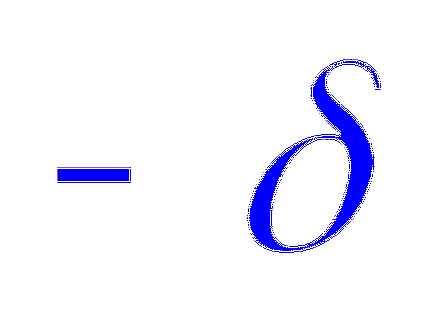
ole creat fiecare uniformă plan. Astfel, din avion cu taxa + Liniile de alimentare du-te, și cu taxă - o parte a planului. Prin urmare, câmpul electric din interiorul avionului și anume de două ori mai mult decât pe același plan. avioane de linii electrice exterioare în direcții opuse, adică avioane de tensiune este egală cu zero.

Notă. Dacă luăm în considerare dispunerea reală a două plăci paralele, distanța între care este mult mai mică decât dimensiunea de plăci (plane condensator), câmpul electric din interiorul plăcii închise, iar intensitatea acesteia

f) In mod similar câmpului electric mezhdukoaksialnymi calculat (coaxial) uniform încărcat cu lungimea unui cilindru radiusamii densitate liniară.

ce câmpul E numai între cilindri. Intensitatea acestui câmp

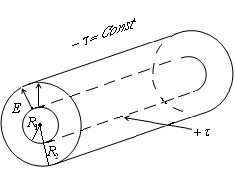
r este distanța de la axa cilindrului.

Când lungimea finală a cilindrului, un astfel de dispozitiv este numit un condensator cilindric.

g) Câmpul dintre cele două sfere concentrice cu radiusamii.

E

Dacă pe sfera suprafețe sunt taxe , întregul câmp Acesta a încheiat numai între suprafețele acestor zone:

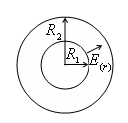
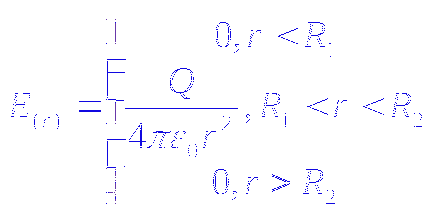
Un astfel de dispozitiv este numit un condensator sferic.