8, câmpul magnetic este curenții rectilinii și circulare
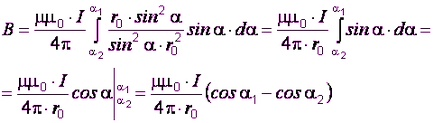
Pentru un conductor infinit lung liniar (1 = 0, 2 = ), ecuația (2.5) devine:
9, Maxwell Ecuații - un sistem de ecuații diferențiale sau formă integrală care descriu câmpul electromagnetic și conectarea acesteia la sarcini electrice și curenți în vid și suport continuu. Împreună cu expresia forței Lorentz. Efecte măsoară valoarea de referință ale câmpurilor electromagnetice asupra particulelor încărcate klassicheskoyelektrodinamiki formează un sistem complet de ecuații. uneori numite ecuațiile lui Maxwell - Lorentz. Ecuațiile sformulirovannyeDzheymsom Clerk Maxwell pe baza acumulate de la mijlocul secolului al XIX-lea a rezultatelor experimentale au jucat un rol-cheie în dezvoltarea de idei ale fizicii teoretice și a avut un puternic adesea decisiv, influența, nu numai cu privire la toate domeniile fizicii, este direct legată de electromagnetism. dar multe au apărut ulterior teorie fundamentală, subiectul nu poate fi redus la electromagnetism (unul dintre exemplele cele mai izbitoare aici poate sluzhitspetsialnaya teoria relativității).
10, sarcină electrică (cantitate electrică) - este valoarea fizicheskayaskalyarnaya. determinarea capacității organismelor de a fi o sursă de câmpuri electromagnetice și să participe la interacțiunea electromagnetică. Pentru prima dată o sarcină electrică a fost introdusă în legea lui Coulomb în 1785.
Unitatea de măsură a taxei în Sistemul Internațional de Unități (SI) - pandantiv - sarcină electrică care trece prin secțiunea transversală a conductorului la un curent de 1 A pentru un timp de 1 s. Încărcați într-un pandantiv foarte mare. Dacă doi purtători (q1 = q2 = 1 C) poziționat în vid, la o distanță de 1 m, s-ar interacționa cu siloy9 10 9 H. adică forța cu care gravitația Pământului ar atrage un obiect cu o masă de ordinul a 1 milion de tone .
sarcină electrică sistem închis [6] este stocat în timp și cuantificată - schimbarea porțiuni, sarcină electrică elementară multiple. adică, cu alte cuvinte, suma algebrică a organismelor sarcini electrice sau de particule, formând un sistem izolat electric nu este schimbat la toate procesele din sistem.
In acest sistem se pot forma noi particule încărcate electric, cum ar fi electronii - datorită fenomenului de ionizare a atomilor sau moleculelor, ioni -. Din cauza fenomenului de disociere electrolitica, etc. Cu toate acestea, în cazul în care sistemul este izolat electric, atunci suma algebrică a taxelor tuturor particulelor, inclusiv proaspetei care apare într-un astfel de sistem este întotdeauna zero.
Un punct de încărcare. legea lui Coulomb - legea fundamentală a electrostatics.
O taxă punct - este încărcat electric. atunci când dimensiunea corpului pe care se concentrează taxa, este mult mai mică decât distanța dintre corpurile încărcate.
Interacțiunea dintre două sarcini punct în repaus definește legea fundamentală a electrostatics - legea lui Coulomb. Această lege a stabilit experimental în 1785 de către fizicianul francez Charles Augustin Coulomb (1736-1806). Formularea legii lui Coulomb, după cum urmează:
Punct de alimentare vzaimodeystviyadvuh fix corpuri încărcate într-un vid este direct proporțională cu produsul dintre modulele de încărcare și invers proporțională cu pătratul distanța între acestea.
Această forță de interacțiune numit Coulomb vigoare. legea lui Coulomb, iar formula va fi după cum urmează: F = k · (| q1 | · | q2 |) / în cazul în care R2 | q1 |, | q2 | - module de sarcină, r - distanța dintre taxe, k - factorul de proporționalitate.
Coeficientul k în SI, de obicei, scris sub forma: k = 1 / (4πε0ε) unde ε0 = 8,85 * 10 -12 C / N * m 2 - constanta dielectrică, ε - constanta dielectrică a mediului.
Pentru ε vid = 1, k = 9 x 10 9 Nm / Cl2.
În cazul în care două sarcini punctiforme sunt plasate în dielectric și distanța dintre aceste taxe la un limite dielectric este semnificativ mai mare decât distanța dintre taxele, forța dintre ele este egal cu: F = [1 / (4πε0)] · [(| q1 | · | q2 |) / R2 ] = k · (1 / π) · [(| q1 | · | q2 |) / r2]
Densitatea de încărcare volum (r),
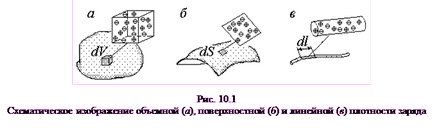
Pentru un obiect liniar (de exemplu, în cazul zaryazhennogosterzhnya) a introdus conceptul de zaryadaτ densitate liniară (ris.10.1, c),
. unde l este lungimea întregului obiect liniei (10.1.1)
în cazul în care dq - taxa pe unitatea de lungime dl.
Dacă obiectul bidimensional (de exemplu, în cazul unui conductor încărcat) a introdus densitatea de încărcare de suprafață (ris.10.1 b)
în cazul în care DQ - taxa prezent pe DS element de suprafata.
Pentru obiecte tridimensionale se administrează o densitate de încărcare de volum (ris.10.1 a)
în cazul în care DQ - volum mic corp încărcat cu celule de încărcare dV.
Câmpul electrostatic poate fi reprezentat grafic prin intermediul liniilor de forță (linii de tensiune). Liniile de alimentare este o curbă a cărei tangentele la fiecare punct coincide cu vectorul intensitate E.
Liniile electrice sunt conceptul convențional și nu există cu adevărat. Liniile electrice și o singură sarcină negativă unică pozitivă - o linie dreaptă radială, lăsând o sarcină pozitivă sau mergând la sarcina negativa.
Dacă densitatea și direcția liniilor de câmp în jurul volumului câmpurile rămân neschimbate, câmpul electrostatic se presupune a fi uniform (= const). De exemplu, taxa este distribuit uniform pe un plan infinit, creează un câmp electric uniform ale cărui linii de forță sunt reprezentate prin linii drepte paralele echidistante.
Pentru a caracteriza liniile de forță nu numai direcția câmpului, dar, de asemenea, puterea, numărul de linii pentru a fi numeric egală cu intensitatea câmpului.
Numărul de linii de câmp care pătrunde către elementul de suprafață dS a, perpendicular pe aceasta, determină vectorul de curgere al intensității câmpului electrostatic:
unde - proiecția vectorului E în direcția n normal la Ds zona
fondant în consecință vectorul E printr-o suprafață închisă arbitrar S
În diferite zone ale suprafeței S este nu numai amploarea, ci și semnul fluxului poate varia:
3), aceasta înseamnă că glisiera linie de-a lungul suprafeței, fără a trece-l.