Calcularea zonelor de figuri plane folosind integralele

În această lecție vom învăța să calculeze aria cifrelor plane. care sunt delimitate de axa abscisei (Ox), segmente de linie dreaptă x = a. x = b, iar programul continuă și non-negativ funcția y = f (x) pentru valorile de "X", în intervalul [a. b]. Această cifră se numește un trapez curbilinie. segmente laterale pot degenera într-un punct. S de această dimensiune trapez curbiliniu poate fi calculată cu ajutorul formulei

Astfel, integrala definită a unei funcții continue nenegativă f (x) pe [a. b] (graficul funcție situată deasupra axei Ox) este numeric egală cu aria trapezului curbat cu o bază [a. b]. Grafic delimitate deasupra funcției y = f (x). Acesta este sensul geometric al integralei definit. Desene de figuri - în exemple.

Dacă f (x) ≤ 0 (graficul funcției este situat sub axa Ox), aria trapezului curbată poate fi calculată cu ajutorul formulei

Există cazuri în care atât limitele superioare și inferioare ale figurii - funcția, respectiv, y = f (x) și y = φ (x). aria figurii calculată cu formula

Astfel, calculul zonelor de figuri plane - una dintre cele mai importante aplicații în care integrala definită este aplicația cea mai fructuoasă. Tot ce a examinat datele din geometria elementară, care permite să se calculeze aria de forme rectilinii - dreptunghiuri, triunghiuri și poligoane. În ceea ce privește formele curbe, există pentru a găsi zona mijloacelor de geometrie elementara nu mai este suficient. Deci, la afaceri. Aflați cum să aplice ceea ce este stabilit în partea de sus a acestui articol.

Începem cu cazul în care zona cifra poate fi calculată prin formula (1).

Exemplul 1. Găsirea zona figurii delimitate de funcția program, axa abscisei (Ox) și liniile drepte x = 1. x = 3.

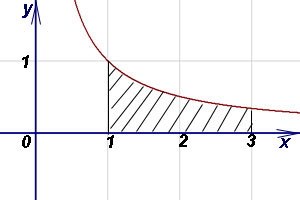
Decizie. Deoarece y = 1 / x> 0 în intervalul [1; 3]. aria trapezului curbiliniu găsită prin formula (1):

Exemplul 2. Găsiți aria figurii delimitate funcție grafic liniar x = 1, iar axa absciselor (Ox).

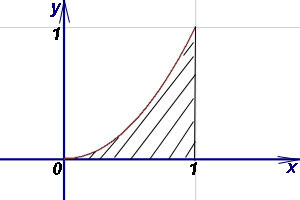
Decizie. Conform formulei (1), avem

În cazul în care s = 1/2; în cazul în care s = 1/3. etc.

Exemplul 3. Găsiți aria figurii delimitate de funcția program, axa abscisei (Ox) și o linie dreaptă x = 4.

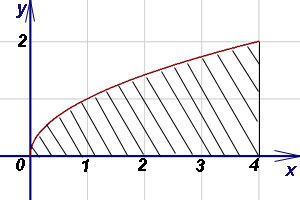
Decizie. Figura Căutând - trapez curbilinie, care a lăsat segment a degenerat la punct. Limitele de integrare sunt 0 și 4. Deoarece, în conformitate cu formula (1) găsi zona trapezului curbiliniu:

Exemplul 4. Găsiți zona cifra mărginită de linii și situate în primul cadranului.

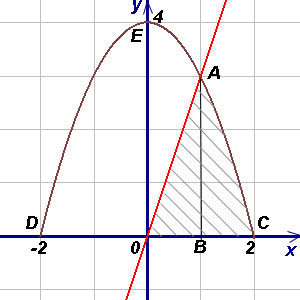
Decizie. Pentru a utiliza formula (1) reprezintă suprafața formei dorite sub forma sumei ariilor triunghiurilor OAB și trapezoid curbilinie ABC. La calcularea ariei unui OAB triunghi limitele de integrare sunt abscise ale punctelor O și figurile A. și pentru ABC - abscisă punctele A și C (A este punctul de intersecție al parabolei și linia dreaptă OA și C - punctul de intersecție cu parabolei axa Ox). Rezolvarea (ca sistem) a unei linii drepte și a unei parabole, obținem (abscisa punctul A) și (abscisa alt punct de intersecție a unei linii drepte și a unei parabole, care nu este necesară pentru decizia). In mod similar, obținem (abscisă punctele C și D). Astfel, avem totul pentru a găsi zona a figurii. am găsit:

Exemplul 5. Găsiți zona ACDB trapez curbilinie. dacă ecuația CD-ului curbei și abscisa A și B, respectiv, 1 și 2.

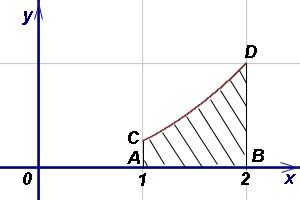
Decizie. Exprimă prin ecuația curbei y: Zona trapez curbiliniu găsită prin formula (1):

Ne întoarcem la cazurile în care suprafața figurii poate fi calculat prin formula (2).

Exemplul 6. Găsiți aria figurii delimitate de parabolei și axa abscisă (Ox).

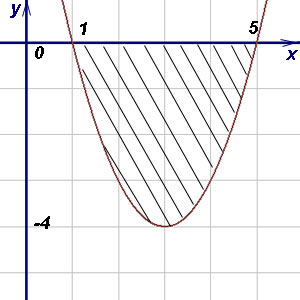
Decizie. Această cifră este situată sub axa x. Prin urmare, pentru a calcula aria de utilizare (2). Limitele de integrare sunt abscisa și punctele de intersecție cu axa Ox parabole. Prin urmare,

Exemplul 7. Găsiți zona, închisă între axa abscisei (Ox) și cele două valuri de sine învecinate.

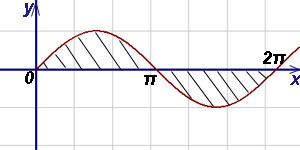
Decizie. Suprafața acestei figuri poate fi găsită prin formula (2):

Să ne găsim fiecare termen:

În cele din urmă vom găsi zona:

Exemplul 8. Găsiți aria figurii, și încheiat între curba parabolei.

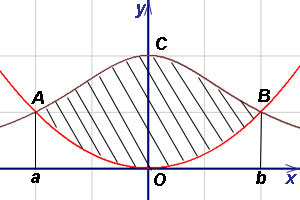
Decizie. Ne exprimăm ecuația linie în ceea ce privește y:

Aria de sub formula (2), cum se obține

în cazul în care a și b - abscisă din punctele A și B. Noi le găsim, rezolvarea ecuațiilor:

În cele din urmă vom găsi zona:

În cele din urmă, cazurile în care suprafața figurii poate fi calculată din formula (3).

Exemplul 9. Găsiți aria figurii delimitată de graficele funcțiilor, și direct și.

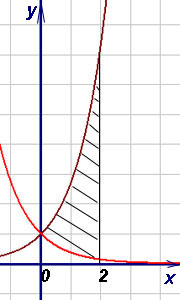
Decizie. Deoarece intervalul [0, 2]. apoi, folosind formula pentru a găsi zona (3), obținem

Exemplul 10. Găsiți aria figurii, și încheiat între parabole.

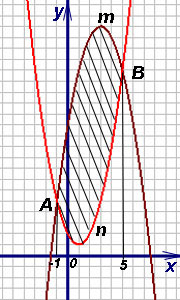
Decizie. AMBN necesare pentru a calcula aria figurii. în care segmentele laterale au degenerat la punctul A și parabole intersecția B. Rezolvarea (după cum este necesar) ecuația parabolei, descoperim abscise și. In intervalul [-1, 5] obținem. Prin urmare, formula (3) găsim aria figurii:

Exemplul 11. Găsiți aria figurii, încheiat între o parabolă și o linie dreaptă.

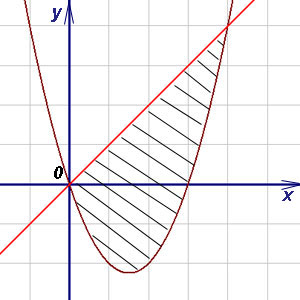
Decizie. Găsim abscisa punctelor de intersecție a unei parabole și o linie dreaptă și. Deoarece intervalul [0, 4]. cu formula (3) găsim aria figurii: