Cum se calculeaza aria figurii folosind definită integrantă

Acasă | Despre noi | feedback-ul

Vom continua să ia în considerare aplicarea de calcul integral. În această lecție, vom discuta tipurile și problema cea mai comună de calcul a zonei unei figuri plane, cu ajutorul integralei bine definit. În cele din urmă, toate în căutarea sensul în matematici superioare - dar îl găsesc. Nu se știe niciodată. Va trebui să se apropie de viață aici, în funcții elementare zonă suburbană și de a găsi zona prin intermediul unui integrala definită.

Pentru a stăpâni cu succes materialul, trebuie:

1) Înțelegerea nedefinită integrală cel puțin la nivelul mediu. Astfel, fierbător de apă ar trebui să devină mai întâi familiarizați cu lecția integrală nedefinită. Exemple de soluții.

2) Pentru a putea aplica formula Teorema fundamentală și se calculează precis integrală. Stabilirea de relații calde și prietenoase cu anumite integralele integrala definită poate fi pe pagină. Exemple de soluții. Sarcina „pentru a calcula suprafața folosind definită integral“ implică întotdeauna desenul de construcție. Prin urmare, o problemă importantă va fi, de asemenea, cunoștințe și abilități de desene de construcție dumneavoastră. La un nivel minim, ar trebui să fie capabil de a construi o linie dreaptă, și parabolic hiperbolă.

Să începem cu un trapez curbat. Curbiliniu trapez - o figură plană delimitată de graficul unei funcții y = f (x), axa OX și liniile x = a; x = b.

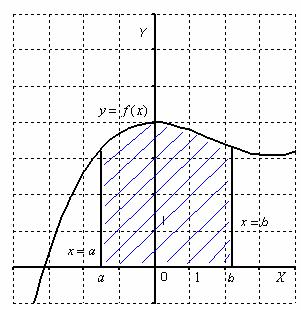
Zona trapezului curbilinie este numeric egal cu definit integralei

Orice integrala definită (care există) are o semnificație geometrică foarte frumos. La lecția definită integrală. Exemple de soluții, am spus că definit integrală - acest număr. Și acum e timpul să recunoaștem un fapt mai util. Din punct de vedere al geometriei integrala definită - un spațiu. Aceasta este, integrala definită (dacă există) corespunde geometric în zona unor figuri. Luați în considerare definit integralei

definește o curbă în plan (dacă se dorește poate fi trase), iar integrala definită este numeric egală cu suprafața trapezului curbiliniu corespunzătoare.

Se calculează aria figurii delimitată de liniile. . . .

Aceasta este o formulare tipică a sarcinii. Cel mai important moment al deciziei - construcția desenului. Mai mult decât atât, desenul trebuie să fie construite în mod corespunzător.

În construcția de desen, am recomandăm următoarea procedură: în primul rând, pentru a construi o mai bună toate liniile (dacă există), și numai atunci - Parabolă, hiperbolă, grafice alte funcții. Prin construcția tehnica pointwise pot fi găsite în Diagramele materiale de referință și proprietăți ale funcțiilor elementare. Acolo puteți găsi foarte utile în ceea ce privește lecția - cum să construiască rapid o parabole.

În această problemă, o soluție ar putea arata.

Efectuați desen (rețineți că ecuația y = 0 specifică axa OX):

Hatch trapez curbilinie nu, aici este evident ce fel de zona în cauză. Decizia continuă:

La [-2; 1] graficul y = x 2 + 2 situat deasupra osyuOX. Prin urmare:

Cei care au dificultăți cu calcularea utilizării integrale și definit de formula Newton-Leibniz

Consultați integrala definită de curs. Exemple de soluții. Odată ce lucrarea se face, este întotdeauna util să se uite la desen și dau seama dacă răspunsul real, dovedit. În acest caz, „cu ochiul liber“ contoriza numărul de celule din desen - bine, aproximativ 9 dactilografiată, similar cu adevărul. Este clar că, dacă ne-am întors, să zicem, răspunsul este de 20 de unități pătrate, atunci este clar că undeva o greșeală - în figura considerată a 20 de celule este în mod clar nu se potrivesc, de la o duzină de forțe. În cazul în care răspunsul dovedit negativ, sarcina este de asemenea rezolvată corect.

Se calculează aria figurii delimitate de xy = 4, x = 2, x = 4 și axa OX.

Acesta este un exemplu pentru soluțiile independente. Soluții complete și răspunsuri la sfârșitul lecției.

Ce se întâmplă dacă trapezul curbilinie este sub osyuOX?

Se calculează aria figurii delimitată de liniile y = e - x. x = 1 și axele de coordonate.

Soluție: desen:

În cazul în care trapez curbilinie se află în întregime sub axa OX. că suprafața sa poate fi găsită prin formula:

În acest caz:

Atenție! A nu se confunda cele două tipuri de probleme:

1) În cazul în care vi se cere să rezolve o parte integrantă definită fără sens geometric, acesta poate fi negativ.

2) În cazul în care vi se cere să găsească aria figurii folosind definită integral, zona este întotdeauna pozitiv! Acesta este motivul pentru care doar considerat formula apare negativ.

În practică, de multe ori o figură și dispus în partea superioară și în jumătatea inferioară, și, prin urmare, de la școala elementară zadachek apelează la mai multe exemple semnificative.

Găsiți aria unei figuri plane delimitată de liniile y = 2x - x 2. y = -x.

Soluție: În primul rând, trebuie să efectuați desen. În construcția desenului în problemele din zonă ne interesează cel mai mult în intersecția liniilor. Vom găsi punctul de intersecție al parabolei y = 2x - x 2 și o linie dreaptă y = -x. Acest lucru se poate face în două moduri. Prima metodă - analitică. Rezolvăm ecuația:

Prin urmare, limita inferioară de integrare, a = 0, limita superioară a integrării b = 3. Cel mai avantajos și de a construi mai repede linia pointwise, limitele de integrare fiind investigate ca și în cazul în care „ei înșiși“. Cu toate acestea, metoda analitică de a găsi limitele încă mai trebuie uneori să se aplice în cazul în care, de exemplu, graficul este suficient de mare, sau de construcție potochennoe nu a dezvăluit limitele de integrare (care poate fi fracționată sau irațională). Ne întoarcem la sarcina noastră: de a construi o primă linie rațională și apoi parabolei. Efectuați desen:

Din nou, clădirea în limitele pointwise de integrare de multe ori clarificat „avtomatomaticheski“.

Acum formulă de lucru:

Dacă intervalul [a; b] o funcție f continuă (x) este mai mare sau egală cu o funcție g continuă (x), suprafața corespunzătoare a figurii poate fi găsită prin formula:

Nu există nu mai este nevoie să se gândească, în cazul în care cifra - deasupra axei sau sub axa, dar este important ceea ce graficul de mai sus (în raport cu o altă diagramă), și care - de mai jos.

În acest exemplu, este evident că pe intervalul [0; 3] parabolei este situată deasupra liniei drepte, și, prin urmare, de 2x - x 2 trebuie scăzută -x.

Finalizarea soluției ar putea arata astfel:

figura Favorizate delimitat de parabolei y = 2x - x 2 de mai sus și y = -x direct de mai jos.

In intervalul [0; 3] 2x - x 2 ≥ -x. Prin care corespunde formulei:

De fapt, formula școlară pentru aria trapezului curbată în jumătatea inferioară (vezi Exemplul №3.) - un caz special cu formula

Deoarece axa OX este dată de ecuația y = 0, o reprezentare grafică a funcției g (x) este situat sub axa OX.

Și acum câteva exemple pentru soluții individuale

Găsiți zona delimitată de cifra

Găsiți zona delimitată de cifra

În cursul soluționării problemelor în calculul zonei cu ajutorul integrala definită se întâmplă incidente, uneori amuzant. Desenul este stabilit în mod corespunzător - dreapta, dar, din neatenție, ... Găsiți zona cifrelor greșite.

În continuare, un caz real:

Se calculează aria figurii delimitată de liniile. . . .

În primul rând, efectuați desenul:

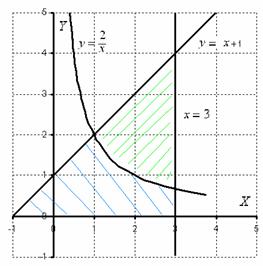
Cifra, care este o zonă de care avem nevoie pentru a găsi un albastru umbrit (uita-te cu atenție la starea - ceea ce figura este limitată). Dar, în practică, din cauza neglijenței, de multe ori decide că aveți nevoie pentru a găsi zona a figurii, care este umbrită în verde!

Acest exemplu este, de asemenea, utilă în faptul că a considerat zona figura cu două integralele definite. într-adevăr:

1) pe intervalul [-1; 1] peste axa OX este linia graficului y = x + 1;

2) pe intervalul [1; 3] de-a lungul axei OX este un grafic hiperbolă y = (2 / x).

Este evident că zona poate (și ar trebui) adauga, astfel:

Se calculează aria figurii delimitate de

Noi reprezentăm ecuația în „școala“ ca

și de a efectua un desen pointwise:

Din figură este clar că limita superioară a noastră „bun»: b = 1.

Dar ceea ce este limita inferioară. În mod evident, acest lucru nu este un număr întreg, dar ce?

Poate, o = (- 1/3)? Dar, în cazul în care este garanția că desenul este executat cu o precizie perfectă, poate fi bine ca a = (- 1/4). Și dacă am greșit a fost reprezentată grafic?

În astfel de cazuri, trebuie să-și petreacă timp suplimentar și să specifice limitele de integrare analitic.

Vom găsi punctul de intersecție a graficelor

Pentru a face acest lucru, vom rezolva ecuația:

Prin urmare, o = (- 1/3).

O altă soluție este banală. Principalul lucru este să nu se piardă în substituții și semne. Calculele nu sunt foarte simple. pe intervalul

cu formula:

În încheierea lecției, ia în considerare cele două sarcini dificile.

Se calculează aria figurii delimitate de

Soluție: Să ne reprezinte această cifră în desen.

Pentru punctul de la punctul de construcție al desenului trebuie să cunoască apariția unui val de sine. În general, este util să se cunoască listele de toate funcțiile elementare, precum și unele dintre valorile sinusul. Ele pot fi găsite în tabelul de valori ale funcțiilor trigonometrice. În unele cazuri (de exemplu, acest lucru) a permis construirea desenelor schematice, în care, în principiu, ar trebui să fie afișate corect grafice și limitele de integrare.

La exterior nu sunt probleme de integrare, ei urmează direct de condiția:

- "X" variază de la zero la "pee". Vom lua o decizie în continuare:

In intervalul [0; π] graficul y = sin x 3 este situată deasupra axei OX. Prin urmare:

(1) În ceea ce sinus și cosinus integrat în puteri ciudat, este posibil să se vadă integralelor lecția funcțiilor trigonometrice. Strangulează un sinus.

(2) Folosind identitatea trigonometric generală

(3) efectuează schimbarea t variabilei = cos x. atunci:

Noi etapele procesului de integrare:

Cine face lucruri rele cu substituții, vă rugăm să mergeți la metoda de înlocuire clasă în nedefinită integrală. Acest lucru nu este algoritmul de înlocuire foarte clar într-o integrală definită, accesați definit integralei. Exemple de soluții.

(4) Aici folosim proprietatile integralei definit

introducerea limitelor de integrare în ordinea „obișnuită“

Se calculează aria figurii delimitate de

Acesta este un exemplu pentru soluțiile independente. O soluție completă și răspunsul de mai jos.

Să considerăm un exemplu interesant de la Arccotangent:

Se calculează aria figurii delimitate de

și axele de coordonate. Soluția completă nu va fi. Răspuns corect:

Exemplul 2: Soluție: desen:

In intervalul [2; 4] graficul y = 4 / x este situată deasupra axei OX, prin urmare:

Notă: Problema găsirii profesorilor zone de multe ori trebuie să înregistreze răspunsul este nu numai exacte, ci și, în special, aproximativ.

Exemplul 5. Soluție: desen:

In intervalul [-1; 3]. . cu formula:

Exemplul 6: Soluție: Efectuați desen.

In intervalul [1; 3] (4 x) ≥ (3 / x), prin care corespunde formulei:

Exemplul 10: Soluție: Noi reprezentăm această cifră în desen:

Pe graficul segmentului este situat deasupra axei. Prin urmare:

Notă: Observați cum integralei este luat din tangenta în cubul, am folosit consecința principală a identităților trigonometrice

Mai mult, în integralele metodei sumãrii funcțiilor sub semnul diferenței (poate fi utilizat în înlocuirea definit integral, dar decizia va fi mai mare).