Distribuția de încărcare de pe suprafața conductorului
În cazul unei distribuții de echilibru a taxelor conductorului sunt distribuite într-un strat subțire de suprafață. De exemplu, în cazul în care conductorul de a informa o sarcină negativă, apoi din cauza repulsiei forțează elementele acestei taxe, se dispersează pe toată suprafața conductorului.
Un studiu folosind o placă de testare
Pentru a investiga experimental tarifele de pe suprafața exterioară a conductorului sunt distribuite cu ajutorul plăcii de testare așa-numitele. Această placă este atât de mică încât, în contact cu conductorul poate fi considerat ca făcând parte din suprafața conductorului. În cazul în care această placă de a exercita un conductor încărcat, o parte din taxa ($ \ triunghi $ q) se deschide și amploarea acestei taxe este egală cu taxa care a fost pe suprafața plăcii conductor de zone pătrate egale ($ \ triunghi S $).
Apoi, valoarea care este egală cu:
Se numește distribuție densitatea de sarcină de suprafață, la un anumit punct.
Descarcarea printr-o placă electrometru test poate judeca magnitudinea densitatea de încărcare de suprafață. De exemplu, dacă încărcați mingea conductiv, puteți vedea prin metoda de mai sus este aceea că densitatea de încărcare de suprafață de echilibru pe mingea este aceeași în toate punctele. Aceasta este, taxa pe suprafața sferei să fie distribuite în mod egal. Pentru mai multe forme complexe de distribuție conductori încărcați mai dificilă.
Densitatea de suprafață a conductorului
Suprafața fiecărui conductor este un echipotențială, dar, în general, densitatea de distribuție de încărcare pot fi foarte diferite în diferite puncte. Densitatea de distribuție de încărcare de suprafață depinde de curbura suprafeței. Secțiunea a fost dedicată descrie starea conductoarelor în câmp electrostatic, am stabilit că intensitatea câmpului în apropierea suprafeței conductorului este perpendicular pe suprafața conductorului în orice punct și este egal cu modulo:
în cazul în care $ _0 $ - electric constant, $ \ varepsilon $ - constanta dielectrică a mediului. Prin urmare,
\ [\ Sigma = E \ varepsilon _0 \ \ stânga (3 \ dreapta). \]
Cu cât mai mare curbura, cu atât mai mare intensitatea câmpului. Prin urmare, proiecții deosebit de mari pe densitatea de încărcare. Aproape depresiunile din conductorul suprafetele echipotentiale sunt mai puțin. În consecință, intensitatea câmpului electromagnetic și densitatea de încărcare în aceste zone mai puțin. Densitatea de încărcare la un potențial set al conductorului este determinat de curbura suprafeței. Aceasta crește odată cu creșterea numărului și scade odată cu creșterea concavitate. densitate mare de încărcare Mai ales pe vârfurile conductoare. Astfel, intensitatea câmpului la vârful poate fi atât de mare încât se poate produce ionizarea moleculelor de gaz, care înconjoară conductorul. semnul opus al taxei de ioni de gaz (în raport cu conductorul de încărcare) sunt atrase de conductorul, sarcina sa este neutralizat. Ionii de același semn sunt respinse de la conductor „pull“ pentru un molecule de gaz neutru. Acest fenomen se numește vânt electric. Charge conductor scade ca urmare a procesului de neutralizare, este ca și cum se scurge din vârful. Acest fenomen se numește expirarea taxa de vârf.
Am spus că, atunci când facem un fir într-un câmp electric, există o diviziune a sarcinilor pozitive (nuclee) și negative (electroni). Acest fenomen se numește inducție electrostatică. Taxele care apar ca rezultat, numit induse. taxa indusă creează un câmp electric suplimentar.
Acuzațiile câmpului indus îndreptate spre direcția opusă a câmpului extern. Prin urmare, taxele care se acumulează pe conductorul, slăbi câmpul magnetic extern.
redistribuire Taxa este, până când se percep taxe pentru condițiile de echilibru a conductoarelor. Cum ar fi câmp dispărând pretutindeni perpendicular în interiorul conductorului și vectorul intensitate a unei suprafețe conductor încărcat. Dacă există o cavitate în conductorul, apoi pentru o distribuție de echilibru a câmpului de încărcare indus în interiorul cavității este egală cu zero. Acest fenomen se bazează protecție ESD. Dacă cineva dorește să protejeze aparatul de câmpurile externe, este înconjurat de un ecran conductor. Într-un astfel de caz, câmpul magnetic extern este compensată în interiorul ecranului apare pe suprafața tarifelor induse. Acest lucru nu poate fi neapărat solidă, dar sub formă de plasă groasă.
Setare: fir lung infinit, încărcat cu o densitate liniară de $ \ tau $, este perpendicular pe planul infinit conduce. Distanța de la filamentul la planul $ l $. Dacă firul continuă să se intersecteze cu avionul în intersecția obține un punct de A. Asigurați-vă în funcție de densitate formula suprafață $ \ sigma \ stânga (r \ dreapta) \ $ taxe induse pe planul de distanța până la punctul A.
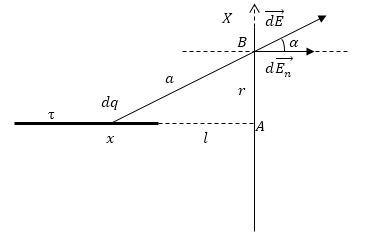
Luați în considerare un punct B, în avion. sârmă lung încărcat la infinit punctul B creează un câmp electrostatic, câmpul este în planul conductor în plan taxele induse formate, care, la rândul său creează un câmp care slăbește filamentul câmpului extern. Componenta normală a planului câmp (cheltuieli induse) la punctul B va fi egal cu componenta normală a firului de câmp la același punct, dacă sistemul este în echilibru. Izolați privind taxa elementară fire ($ dq = \ tau dx, \ în cazul în care \ dx-elementar \ felie \ fir \ $), vom găsi punctul în tensiune creată de această taxă ($ dE $):
Găsim componentă normală a câmpului cu filament membru rezistență la punctul B:
în cazul în care $ cos \ alpha $ exprima ca:
Ne exprimăm distanța $ a $ de teorema lui Pitagora ca:
Substituind (1.3) și (1.4) până la (1.2), obținem:
Găsim integrala (1.5), în cazul în care limitele de integrare de la $ l \ (distanța \ la \ următoarea capăt \ fir \ a \ plan \) \ la \ \ infty $:
Pe de altă parte, știm că domeniul unui plan încărcat uniform este:
Asimilarea (1,6) și (1,7), ne exprimăm densitatea de încărcare de suprafață:
Sarcina: Se calculează densitatea de încărcare de suprafață, care este creat în jurul suprafeței Pământului, dacă intensitatea câmpului Pământului este de 200 $ \ \ frac $.
Presupunem că conductivitatea dielectrică de aer $ \ varepsilon = 1 $ ca în vid. Ca bază pentru rezolvarea problemei va formula pentru calcularea intensității unui conductor încărcat:
Să ne exprimăm densitatea de încărcare de suprafață, obținem:
în cazul în care constanta dielectrică este cunoscută pentru noi și este egal cu SI $ _0 = 8,85 \ cdot ^ \ frac. $
A: Densitatea de suprafață a distribuției de încărcare de suprafață a Pământului este egală cu $ 1,77 \ cdot ^ \ frac $.
Aflați costul de muncă scris la comanda
alte articole
Efectuarea toate tipurile de lucrari de fizica

Suntem deschiși în timpul săptămânii de la 10:00 la 20:00