mișcare rectilinie a unui punct material

Formulele sunt derivate de mișcare rectilinie a trei căi sarcini de mișcare - la coordonate cunoscute, în funcție de timpul; o accelerație cunoscută în funcție de timp și accelerarea coordonatei. Considerată rectilinie uniform rectilinie uniform accelerată mișcare.

Formulele de bază ale mișcării rectilinii

Lăsați un material se deplasează punct de-a lungul liniei. Mai mult, și indică poziția și viteza punctului la momentul inițial.
Dacă modificările legii stabilite coordonatele sale la timp:
.
diferențierea coordonata timpului, vom obține viteza și accelerația punctului:
;
.

Să ne dependența de accelerare a timpului:
.
Apoi, în funcție de viteza și poziția din timp în timp se determină prin formulele:
(1);
(2);
(3);
(4).

Să presupunem că știm dependentă de coordonatele accelerației:
.
Apoi, dependența vitezei de coordonate este după cum urmează:
(5).
Timpul de coordonate se determină în formă implicită:
(6).

Pentru mișcare uniformă rectilinie:
;
;
.

Pentru rectilinie mișcare uniform accelerată:
;
;
;
.

Formulele oferite aici pot fi utilizate nu numai pentru mișcarea rectilinie, dar, de asemenea, pentru unele cazuri de mișcare curbilinie. De exemplu, pentru mișcarea tridimensională într-un sistem de coordonate rectangulare. dacă mișcarea de-a lungul axei este independentă de valorile proeminențelor de pe celelalte axe. Apoi formulele (1) - (6) prevăd valorile proiecțiilor în funcție de axa.

De asemenea, aceste formule sunt aplicabile în timpul deplasării de-a lungul unei căi predeterminate de mișcare în timpul procesului natural de locuri de muncă. Doar aici acționează ca o coordonată de lungimea traseului arcului măsurată de origine selectată. Apoi, în locul proeminențelor și ar trebui să fie substituite și - proiecția vitezei și accelerației pe direcția selectată a tangenta la traiectoria.

mișcarea rectilinie la coordonatele cunoscute, în funcție de timpul

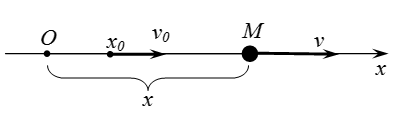
Considerați cazul în care punctul de material se deplasează într-o linie dreaptă. Am ales un sistem de coordonate cu originea într-un punct arbitrar. Axa este direcționată de-a lungul liniei de mișcare a unui punct. Apoi poziția punctului este determinată în mod unic de single de coordonate.

Dacă legea se schimbă coordonatele de timp.
.
apoi de diferențiere în raport cu timpul. Găsim rata de schimbare a legii:
.
Atunci când punctul se deplasează în direcția pozitivă (de la stânga la dreapta în figură). Atunci când punctul se deplasează în direcția negativă a axei (în figura de la dreapta la stânga).

Diferențierea în funcție de timp viteza, descoperim legea schimbării de accelerare:
.
Deoarece linia nu are nici o curbură, raza de curbură a traiectoriei poate fi considerat infinit de mare. Apoi, accelerația este egală cu zero:






.
Acesta este punctul de accelerație tangențial (tangențial)
.
Acest lucru este destul de natural, deoarece atât viteza și accelerația unui punct sunt direcționate tangențial la traiectoria - linia de-a lungul căreia are loc mișcarea.
Dacă același semn (adică, ambele pozitive sau ambele negative), viteza modulului crește (viteza crește în valoare absolută). Dacă semne diferite, atunci modulul scade viteza de (viteza scade în valoare absolută).

mișcare liniară cu o anumită accelerație

Accelerare, dependente de timp

Să ne cunoaștem legea schimbării de accelerare a timpului:
.
Sarcina noastră este de a găsi legea ratei de schimbare și variația coordonatelor de timp:
;
.

Se aplică formula:
.
Aceasta este o primă ecuație diferențială cu variabile separabile. Împărtășim variabile și să integreze:
;
.
Aici - constanta de integrare. Acest lucru arată că numai cunoscut accelerația în funcție de timp, nu se poate identifica în mod unic dependența ratei din timp în timp. Avem o mulțime de schimbări de viteză de legi, care diferă una de cealaltă printr-o constantă arbitrară. Pentru a găsi rata de noi schimba legea, trebuie să ne întrebăm un alt sens. De obicei, această valoare este valoarea vitezei la momentul inițial. Pentru a face acest lucru, continuați de integrala nedefinită la definiția:
.
Să - punctul de viteza la momentul inițial. Înlocuim.
;
;
.
Astfel, modificările vitezei legii din când în când are forma:
(1).

În mod similar, coordonatele definesc legea de variație cu timpul.
.
(2).
Aici - valoarea timpului inițial.

Substituind (1) (2).

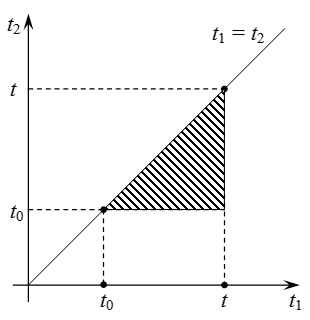
Regiunea de integrare în dublu integralei.

Dacă modificați ordinea de integrare în dublu integralei, obținem:

Astfel, avem următoarea formulă:
(3);
(4).

Coordonatele dependente de accelerare

Să presupunem acum că știm legea schimbării de accelerare a coordonatelor:
.
Avem nevoie pentru a rezolva ecuația diferențială:
.
Această ecuație diferențială nu conține nici o variabilă independentă în mod explicit. Metoda generală pentru rezolvarea unor astfel de ecuații sunt luate în considerare la pagina „de ordin superior ecuații diferențiale care nu conțin variabila independentă în mod explicit.“ Conform acestei metode, noi credem că este o funcție de.
;
.
Împărtășim variabile și să integreze:
;
;
;
.
Având rădăcina pătrată trebuie remarcat faptul că viteza poate fi atât pozitive, cât și negative. O scurtă distanță de punct. semn este determinat de semnul constant. Cu toate acestea, în cazul în care accelerația este îndreptată opusă vitezei, viteza punctului este redusă la zero și direcția de mișcare este inversată. Prin urmare, semnul corect, plus sau minus, este ales în considerarea unui anumit mișcare.
(5).
La începutul mișcării
.

Acum vom determina dependența de coordonatele de timp. Ecuația diferențială pentru coordonatele formei:
.
Această ecuație diferențială cu variabile separabile. Împărtășim variabile și să integreze:
(6).
Această ecuație determină dependența coordonatele timpului implicit.

mișcare liniară uniformă

Să aplicăm rezultatele de mai sus în cazul mișcării uniforme rectilinie. În acest caz, accelerarea
.
În conformitate cu formulele (1) și (2) găsim:
;
. Adică, viteza este constantă, și coordona o funcție liniară de timp. (5) și (6) dau același rezultat.

Rectilinie mișcare uniform accelerată

Acum ia în considerare rectilinie uniform mișcare accelerată.
În acest caz, accelerația este constantă:
.
În conformitate cu formulele (1) și (2) găsim:
;

Dacă aplicăm formula (5), obținem dependența vitezei de coordonate:
.

mișcare liniară în formă vectorială

Formula rezultată poate fi reprezentată în formă vectorială. Pentru a face acest lucru, se multiplica suficient de ecuații definitorii. și vectorul unitate (un vector unitate). direcționat de-a lungul axei.

Apoi, vectorul raza punctului, viteza și accelerație vectorii sunt de forma:
;
;
.