Procedura de soluționare a problemelor pe principiul superpoziției

Acasă | Despre noi | feedback-ul

Sarcina 1.Prochitat; notați toate valorile prescrise ale mărimilor fizice și a le converti la sistemul SI.

· În figură descrie distribuția sarcinilor care produc un câmp;

· Alegeți un sistem de coordonate, ținând seama de simetria problemei;

· Desemnați toate distantele, care sunt necesare pentru rezolvarea problemei, și să atragă intensitatea câmpului generat de vectori fiecare încărcare de distribuție până la punctul de interes.

3. Scrieți formula de calcul câmpurile de tensiune moduli ale taxelor individuale într-un anumit punct.

4. Pentru a proiecta punctele forte ale tuturor vectorilor pe axa de coordonate și pentru a găsi proiecția vectorului total de intensitate pe fiecare axă. Cunoscând proiecția totală a vectorului pe axele de coordonate Ex. Ey și Ez. putem calcula vectorul unitar total folosind teorema lui Pitagora.

Exemple de rezolvare a problemelor în calculul câmpurilor electrice pe baza principiului superpoziției

Găsiți câmpul electric la punctele A și B
(A se vedea. Fig.) Intins pe mediatoare între sarcini punctiforme q1 = 8 nC și nC q2 = -6, sunt în vid. Distanța dintre tarifele r = 10 cm, AB = 4 cm, e = 1.

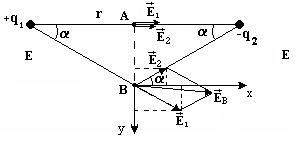
Figura prezintă aranjamentul taxelor și punctele A și B, pentru care trebuie să găsim puterea câmpului, și alegerea sistemului de coordonate prezentat.

a) La punctul Un câmp este creat prin două puncte de taxe și q2 q1. Prin definiție, intensitatea câmpului electromagnetic - este forța cu care unitatea de încărcare generator de câmp funcționează pe o sarcină punct pozitiv, poziționat la punctul A, astfel încât vectorul de tensiune la care punct în aceeași direcție. Tensiunea totală este suma de câmp ale taxelor individuale

sau în proiecție pe axa OX

Scriem formula de calcul amploarea intensității câmpului de sarcini punctiforme și q2 la q1 punctul A:

Și vom ajunge la punctul:

b). La punctul vectorilor B și 2a sunt direcționate la un unghi între ele și modulele vectorilor nu sunt aceleași, deoarece valoarea q1 și taxe diferite q2.

Scriem formula de calcul amploarea taxelor și a punctelor forte q2 câmpului q1 la punctul B:

Fiecare dintre acești vectori oferă o proiecție pe ambele axe:

Proiectii totală vector intensitate la punctul B va fi egal cu:

Acum este posibil să se obțină o formulă de teorema lui Pitagora pentru a calcula modulul vectorului câmpului electric generat la q1 tarifele punctul B și q2. .

Cu toate expresiile obținute prin efectuarea de transformări algebrice, obținem expresia finală pentru calculul cantităților dorite:

Calculăm valoarea numerică a câmpului total de la punctul B:

Notă. În unele cazuri, atunci când o decizie se datorează transformărilor algebrice destul de greoaie, putem efectua calcule în cursul rezolvării problemei. Deci, a fost posibil să se facă, și pentru a rezolva această problemă.

A: intensitatea câmpului electric la punctul A este
EA = 50,4 kV / m și este direcționată de taxa la q2 taxa q1. La punctul B, tensiunea este egală cu U = 24,1 kV / m și este arătat direcția.

3. Exemplul 1. Două fire lungi de cum ar fi incriminați distanțate r1 = 10cm în afară. Densitatea sarcinii liniare sunt identice și egale cu = 10mkKl / m.

Găsiți magnitudinea și direcția intensitatea câmpului rezultant la punctul A, fiecare filament la distanță de la o distanță = 10cm.

câmpuri electrostatice generate de diferite distribuții ale taxelor sunt formate pe principiul superpoziției la fiecare punct în spațiu. Având în vedere simetria problemei, face un desen, plasând firul perpendicular pe planul desenului. Un punct îndepărtat din ambele catene cu o distanță a = r1 .Poluchili triunghi echilateral. Pentru a găsi direcția intensității câmpului vectorial generat în punctul A percepe fiecare filament pus în acest punct taxa de studiu „+1“ și de a determina modul în care câmpurile din fire acționează în această taxă. Deoarece firele sunt încărcate pozitiv, ele vor respinge taxa de testare și vectorul și va fi direcționat așa cum este arătat. Vector intensitatea totală a câmpului, în conformitate cu principiul superpoziției, situat la regula paralelogramului.

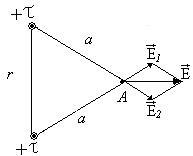
Tăria interacțiunea acestor filamente încărcate depinde de distanța dintre ele, astfel încât funcționarea intensității câmpului electrostatic trebuie calculată prin filamentele integrale când extinse.

1) Se poate observa că indică spre dreapta, iar modulul poate fi găsit ca:

2) Rezistența interacțiunii dintre filamentele încărcate depinde de distanța dintre ele. Fiecare fir creează un câmp, iar acest câmp acționează asupra taxa de un alt fir. - intensitatea câmpului electromagnetic al primei catene.

-forța pe unitatea de lungime a catenei a doua este:

Activitatea acestei forțe poate fi calculată ca:

Să luăm integralei funcției. Toate constantele scoate din semnul integrală și de a obține tabelare integrală, care este egală cu logaritmul natural al argumentului.

Noi substituie limitele de integrare și în final obținem:

Folosind datele problemei, obținem un răspuns numeric

Sarcina pozitivă q = 5 x 10 -8 kD uniform distribuit sârmă fin semiring rază R = 20 cm. Pentru a determina intensitatea câmpului E la centrul semiring.

q = 5 x 10 -8 kD;

Analiză și decizie. În această sarcină, câmpul produs de sarcină q, distribuite pe subțiri semiinelele de rază R. Densitatea sarcinii liniare este :. Pentru un astfel de caz nu se poate utiliza în mod direct cu formula pentru intensitatea câmpului unui punct de încărcare sau filamentul fără sfârșit încărcat. O astfel de problemă poate fi rezolvată folosind principiul superpoziției. Se împarte întregul ghid pe parcele foarte mici de lungime dl. la fiecare taxa de contabilitate dq = t × dl. O astfel de taxă poate fi considerată ca o valoare punct și intensitatea câmpului taxei calculat utilizând formula

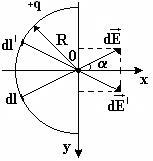
Figura arată selectarea axelor de coordonate și câmpul vectorial. generat la încărcare O .Given simetrie a problemei, care este sistemul asociat cu punctul O, centrul de inele și jumătate coordonate punctul de referință și pentru a transmite axele de coordonate așa cum se arată.

Noi prognozăm vectorul pe axele de coordonate:

Se vede de simetrie ca fiecare sarcină elementară dq este dispus simetric în raport cu axa OX ¢ taxa DQ. Proiecția intensitatea câmpului ale acestor taxe pe axa y va da un zero la toate unghiurile unui.

Astfel, este necesar să se găsească numai proiecția totală a vectorului pe axa x. Se înțelege că, în cazul unei distribuții continue de sarcină ar trebui să fie înlocuită cu însumare de integrare pe întreaga lungime a firului, pe care taxa.

Integrantul include două variabile l și. Având în vedere că, și dl = Rd a, înlocuiți variabila de integrare și de a obține

Figura arată că. a.

A: Intensitatea câmpului în centrul inelului este egală cu 7,2 kV / m.

Figura prezintă un plan infinit încărcat cu planul suprafeței încărcăturii SCLC s = 40 / m2, și cum ar fi încărcat talon cu o masă m = l g și încărcare q = 1 nC. Ce unghi a cu avionul formează un fir pe care mingea agățat?

Taxa este în planul terenului. Acesta funcționează pe puterea de trei mingii reprezentate în Fig. Scriem starea echilibrului mingii.

Noi prognozăm ecuația rezultată pentru axele de coordonate:

Rezolvarea sistemului de ecuații, obținem Fel. = Mg × tga. .

Pe de altă parte, Fel. = QE. unde E - câmp electric creat de un plan infinit.

Din sistemul de ecuații rezultat avea

Câmpul plan infinit poate fi exprimat după cum urmează:

În acest caz, taxa și planul în aer, adică e = 1.

tga = 0,2259 »0226

A: Firul este unghiul plan a = 13 0.