Zona cifra mărginită de linii

Instrucțiuni. Pentru soluții intră funcția în formă y = f1 (x); y = f2 (x).

Exemplul №1. Se calculează aria figurii delimitate de linii și x + y = 6.
Decizie. Noi construim un sistem de coordonate xOy aceste linii. Vom găsi punctul de intersecție al acestor linii

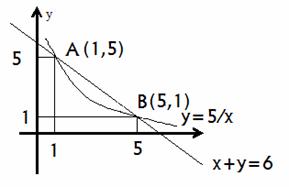
Fig.1. forme pătrate.

Vom nota aceste puncte cu A și B. Astfel, A (1, 5), B (5; 1). Zona de căutare S este egală cu diferența dintre pătrate ale figurii delimitate de liniile x = 1, x = 5, y = 0, y = 6-x (notat zona prin S1), iar liniile x = 1, x = 5, y = 0, (aceasta zona notată S2). astfel
S = S1 - S2
S2 Zona poate fi calculată cu ajutorul definit integralei
2 unități.
Zona S1 poate fi calculată ca suma pătratelor unui triunghi dreptunghic și un dreptunghi, dar încă mai convenabil pentru a calcula S1 integrală
.
Acum puteți calcula suprafața necesară
S = S1 - S2 = 12-5 LN5
Răspuns: S = 12 - 5 LN5 unități 2.