Zona de funcții și o gamă de exemple de funcții
principal nbsp> nbsp Wiki-Tutorial nbsp> nbsp matematică nbsp> clasa nbsp9 nbsp> nbspFunktsiya: valori de domeniu și gamă de funcții + EXEMPLE
Funcția este un model. Definim X, setul de valori ale variabilei independente // independent -Deci orice.
O funcție este o regulă prin care fiecare valoare a variabilei independente în setul X poate fi găsit doar variabila dependentă. // și anume pentru fiecare x este unul apropiat.
Definiția sugerează faptul că există două variabile independente ponyatiya- (care este notat cu x și poate lua orice valoare) și variabila dependentă (care este notat cu y sau f (x) și se calculează dintr-o funcție când înlocuim x).
1. Independent este x, atunci ia orice valoare, fie x = 3
2. Acum și y compute, atunci y = x = 5 + 5 + 3 = 8. (În funcție de x, pentru ca un substitut x, y, și așa obținem)
Se spune că variabila y este dependentă funcțional asupra variabilei x și se notează astfel: y = f (x).
2. y = x ^ 2. (Chemat. Parabolă)
3.u = 3 + 7. (Chemat. Linie)
4. y = √ x. (Chemat. Ramură Parabolă)
Variabila independentă (cat. Numim x) este numele argumentului funcției.
Domeniul funcției
Setul de valori luate de argumentul funcției, denumit domeniul definirea funcției și este notat cu D (f) sau D (y).
Luați în considerare D (y) pentru 1., 2., 3., 4.
1. D (y) = (∞, 0) și (0, + ∞) // set toate numerele reale cu excepția punctului zero.
2. D (y) = (∞ + ∞) // toate deystvit.chisel plural
3. D (y) = (∞ + ∞) // toate deystvit.chisel plural
4. D (y) = [0; + ∞) // mn de neotritsat.chisel
Variabila dependentă (cat. Numim y) este numele valorii funcției.
valori de câmp ale
Setul tuturor valorilor care poate lua variabila dependentă, numită domeniul valorilor funcției și este notat cu E (f) sau E (y).
Luați în considerare E (y) pentru 1., 2., 3., 4.
1. E (y) = (∞, 0) și (0, + ∞) // set toate numerele reale cu excepția punctului zero.
2. E (y) = [0; + ∞) // mn de neotritsat.chisel
3. E (y) = (∞ + ∞) // toate deystvit.chisel plural
4. E (y) = [0; + ∞) // mn de neotritsat.chisel
Luați în considerare exemplele de mai
1) Declarația problemei. Găsiți funcția y = 4 / (3 + x)
1. Găsiți D (unde Y) // adică. Ce valori pot x. în acest scop, vom găsi TCC (interval fracțiune de valori admise)
înseamnă D (y) a funcției (∞, 3) și (3; + ∞) // set toate numerele reale, altele decât cele trei.
2. Găsiți E (y) // de exemplu. Ce valori pot avea, pentru toate x posibile
rezolva o ecuație de forma 4 / (3 + x) = A, unde A Je E (y)
Aceasta înseamnă E (y) a funcției (∞; 4) și (4 + ∞) // set toate numerele reale, altele decât cele patru.
2) Declarația problemei. Găsiți D (y) și E (y) a funcției prezentată în graficul
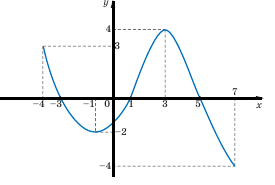
definition câmp (valoarea x) este aspectul intervalului axei x [4; 7]
Valori de domeniu (valori y) caută y este valoarea [4; 4].