seria numerică, matematică, soluție on-line!
matematică grecești sunt în mare parte dominate de geometria și de mult timp petrecut numărarea numărului de puncte aranjate într-un plan în formă de diferite forme geometrice. Numărul de puncte care constituie
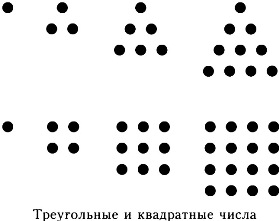
Se poate imagina triunghi sverhmikroskopichesky constând dintr-un singur punct. Trei puncte formează, de asemenea, un triunghi în care două puncte de pe fiecare parte. Șase puncte formează deja un triunghi mai mare a cărui trei puncte de pe fiecare parte, și zece puncte - un triunghi, ale cărui patru puncte de pe fiecare parte.
Pot fi scrise într-un număr de numere triunghiulare: 1, 3, 6, 10, 15, 21. 28, 36, 45, 55 și așa mai departe. Fiecare număr succesiv de forme triunghiulare un triunghi, în care pe fiecare parte, la un singur punct mai mult. Un număr de numere triunghiulare este fără sfârșit.
Vă rugăm să rețineți, o serie de numere triunghiulare formează o anumită dependență. Primul număr este egal cu 1, ce urmează este 3, adică, 1 + 2, urmat de 6, adică, 1 + 2 + 3, apoi 10, adică 1 + 2 + 3 + 4, apoi 15, adică, 1 + 2 + 3 + 4 + 5, și așa mai departe. Memorând această relație, va fi capabil să continue seria de numere triunghiulare pe termen nelimitat, fără a face triunghiuri și puncte de numărare. Determina dacă numărul dat de triunghiulare sau nu, este posibil, prezentându-l sub forma unei serii, similar cu cele de mai sus. În cazul în care numărul poate fi reprezentat ca suma de numere în care fiecare număr succesiv este unul mai mare decât cea anterioară, iar primul număr este identitatea, atunci acest număr - triunghiular.
Orice grup de numere care pot fi reprezentate ca o secvență de ascultare într-o anumită regulă, formează o serie de numere.
Numerele sunt numărul de puncte de la care se poate face un pătrat, poate fi, de asemenea, reprezentat ca o serie. Ca și ultima dată, un punct poate fi considerat ca cuplu sverhmikroskopichesky
rehugolnik. Patru puncte formează, de asemenea, un patrulater. în care la două puncte de pe fiecare parte. Nouă puncte formă are un dreptunghi mai mare, în care la trei puncte de pe fiecare parte, în timp ce șaisprezece puncte - patrulater ale cărui patru puncte de pe fiecare parte.
Pot fi scrise într-un număr de patrulater: 1, 9, 16, 25, 36, 49 și așa mai departe. Fiecare număr succesiv de quadrangular formează un patrulater care pe fiecare parte, la un singur punct mai mult. Un număr de numere dreptunghiulare este fără sfârșit.
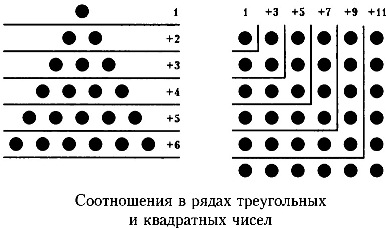
După analizarea numerele care alcătuiesc seria de numere cvadruple, vom vedea că ele sunt, de asemenea, supuse la o anumită relație. Să începem cu 1. Nu există opțiuni, unitatea - este doar unul. Dar, 4 + 1 = 3, apoi 9 = 1 + 3 + 5, = 1 + 16 3 + 5 + 7 și așa mai departe.
Raportul dintre numărul de rânduri triunghiulare și pătrat-picior indicate în diagramă.
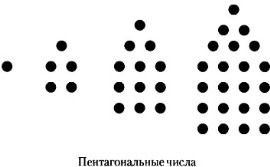
Grecii au avut o serie de numere pentagonale. care sunt prezentate în figură. Această serie poate fi văzută ca o sinteză a seriilor triunghiulare și patrulateră. Dacă vom construi câteva pentagoane în același mod ca și triunghiuri construite și dreptunghiuri, obținem seria de numere de forma 1, 5, 12, 22, 35, 51, 70 și așa mai departe. Aceasta este o serie de numere, care sunt preparate prin adăugarea de numere diferă unul de altul prin trei. Primul termen al seriei - o unitate. II - 5, adică 1+ (1 + 3) = 1 + 4. În al treilea rând - 12, adică, + 4 + 1 (4 + 3) = 1 + 4 + 7, a patra - 22, adică, 1 + 4 + 7 + 10 și așa mai departe.
Grecii au inventat și alte forme geometrice. modelarea serie de numere. Numerele care compun aceste secvente, numite buclat. Unii dat numărul de plat simulate nu mai este figuri ca un triunghi și un pătrat, iar volumul, cum ar fi cuburi. Aceste cuburi sunt dificil de a descrie în imagine, dar dacă te uiți la linia numărul, vă puteți face o idee despre forma cubica a punctelor. Seria de numere cubi - un număr de 1, 8, 27, 64, 125 și așa mai departe.
Mai multe numere cubi prezintă, de asemenea, o serie de sume de numere impare. Cu toate acestea, aceste sume nu încep cu unul. Primul termen al seriei - o secundă1 - 8 + 5 sau 3; a treia - este de 27 sau 7 + 9 + 11; În al patrulea rând - este de 64 sau 15 + + 13 17 + 19. Fiecare grup de numere care au nevoie pentru a rezuma, începe cu un număr impar, după cel care completează suma anterioară, iar numărul de termeni în fiecare din următoarele sume la una mai mult decât anterior.
Împărtășește cu prietenii: