vector câmp electric 1
În conformitate cu teoria cu rază scurtă, interacțiunile dintre organismele însărcinate, care sunt la distanță unul față de celălalt, transportate de câmpuri electromagnetice () produse de aceste organisme în spațiul din jur. În cazul în care câmpurile sunt fixate particule (corpuri), câmpul electrostatic este. În cazul în care câmpul nu se schimbă în timp, se numește staționar. Câmpul electrostatic este staționar. Acest câmp - un caz particular al câmpului electromagnetic. Caracteristica de putere a vectorului intensității câmpului electric este utilizat, care poate fi definit ca:
în cazul în care $ \ overrightarrow $ - „proces“, forța exercitată de câmp pe o sarcină q staționar, care este numit uneori Astfel, este necesar să se taxa „test“ a fost mic, astfel încât să nu denatureze câmpul, a cărui intensitate a fost măsurat folosindu-l. Din ecuația (1) arată că tensiunea coincide cu direcția forței cu care câmpul acționează asupra unității pozitiv „taxa de test“.
Intensitatea câmpului electric nu depinde de timp. În cazul în care intensitatea la toate punctele de la fel, câmpul se numește omogen. În caz contrar, câmpul nu este uniformă.
Liniile de forță
Pentru reprezentarea grafică a câmpurilor electrostatice utilizând conceptul de linii de forță.
Liniile de linii de forță de intensitate sau de câmp sunt numite linii ale căror tangentele în fiecare punct al câmpului coincide cu direcția de tensiune la aceste puncte.
Liniile de forță ale câmpului electrostatic sunt acea poziție. Ei încep pe sarcini pozitive și se termină negativ. Uneori, ei pot merge la infinit sau provin de la infinit. Liniile de câmp nu se intersectează.
Vectorul câmpului electric se supune principiului superpoziției, și anume:
Câmpul vectorial rezultat poate fi găsit ca suma vectorială a tensiunii sale câmpuri „individuale“. În cazul în care taxa este distribuită în mod continuu (nu este nevoie să se ia în considerare discretia), intensitatea totală a câmpului există ca:
În ecuația (3), integrarea este realizată pe zona distribuției de încărcare. În cazul în care taxele sunt distribuite pe linia ($ \ tau = \ frac $ o densitate liniară a distribuției de încărcare), integrarea în (3) se realizează de-a lungul liniei. În cazul în care taxele sunt distribuite pe suprafața și densitatea de suprafață a distribuției de $ \ sigma = \ $ Frac, apoi se integreze pe suprafata. Integrarea se realizează asupra volumului, în cazul în care acordul cu distribuția de sarcină spațială: $ \ rho = \ Frac $, în cazul în care $ \ rho $ - densitatea de volum a distribuției de încărcare.
Intensitatea câmpului
Intensitatea câmpului în izolator este egală cu suma vectorială a punctelor forte de câmp care creează sarcini libere ($ \ overrightarrow $) și cheltuielile aferente ($ \ $ overrightarrow):
Foarte des în exemple ne confruntăm cu faptul că dielectric este izotrop. În acest caz, intensitatea câmpului poate fi scris ca:
în cazul în care $ \ varepsilon $ - constantă dielectrică relativă a mediului la un moment dat al câmpului. Astfel, de la (5) care, într-o rezistență dielectric izotrop omogenă a câmpului electric în $ \ $ varepsilon ori mai puțin decât în vid.
Intensitatea câmpului electrostatic a taxelor punct al sistemului este:
În tensiunea sistemului câmp de încărcare punct CGS în vid, este egal cu:
Sarcina: Sarcina este distribuit uniform peste un sfert de cerc cu raza R, cu o densitate liniară $ \ $ tau. Găsiți intensitatea câmpului în punctul (A), care ar fi centrul cercului.
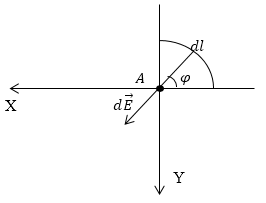
Distingem pe porțiunea încărcată a porțiunii elementare circumferința ($ dl $), care va crea un element de la punctul A, pentru a scrie expresia pentru ea puterea (CGS va folosi sistemul), atunci expresia de $ d \ overrightarrow $ are forma:
Proiecția de $ d \ overrightarrow $ pe axa OX este de forma:
Ne exprimăm dq printr-o taxa de densitate $ \ $ tau liniar:
\ [Dq = \ tau dl = \ tau \ cdot 2 \ pi RDR \ \ stânga (1.3 \ dreapta). \]
Folosind (1.3) transformam (1.2), obținem:
în cazul în care $ cu 2 \ pi = dR d \ varphi $.
Găsim complet de proiecție $ E_x $, integrarea (1.4) peste $ d \ varphi $, în cazul în care unghiul este schimbat $ 0 \ le \ varphi \ le 2 \ pi $.
Să ne vectorul intensitate de proiecție pe axele OY, prin analogie, fără nici o explicație specială, putem scrie:
\ [_ Y = DESIN \ varphi = \ fracsin \ varphi d \ varphi \ \ stânga (1,6 \ dreapta). \]
Integrarea expresiei (1.6), se modifică unghiul de $ \ frac \ le \ varphi \ le 0 $, obținem:
Am găsit magnitudinea intensitatea la punctul A, folosind teorema lui Pitagora:
Răspuns: Intensitatea câmpului în punctul (A) este egal cu $ E = \ frac \ sqrt $.
Target: Localizați câmpul electrostatic este emisfere, a căror rază este egală cu R. Densitatea sarcinii de suprafață este egală cu $ \ sigma $ încărcat uniform.
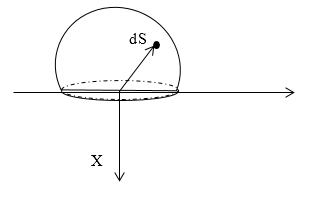
Izolați pe o suprafață a unei sfere elementare taxa de $ dq $ încărcat, care este dispus pe zona elementului dS $ $ În sferice coordonatele $ $ dS este .:
\ [DS = R ^ 2sin \ theta d \ theta d \ varphi \ \ stânga (2.1 \ dreapta) \]
în cazul în care $ 0 \ le \ varphi \ le 2 \ pi, \ 0 \ le \ theta \ le \ frac. $
Scriem expresia pentru punctul intensității câmpului de încărcare elementară în SI:
Vector tensiune de proiectare pe axa OX, obținem:
taxa elementară exprimată în ceea ce privește densitatea de sarcină de suprafață, obținem:
\ [Dq = \ sigma dS \ \ left (2.4 \ dreapta). \]
Înlocuim (2.4) în (2.3), folosind (2.1) Integrarea, obținem:
Ușor pentru a obține că $ E_Y = 0. $
A :. Intensitatea câmpului de suprafață emisfera încărcată în centru este de $ E = \ frac_0> $