Zona cifra mărginită de linii - Forum - Kazahstan și educație - un site educațional

Acum să învețe cum să găsească aria figurii formată din două linii.

Se determină suprafața figurii delimitată de liniile y = x + 3, y = 2-x și axa abscisă.

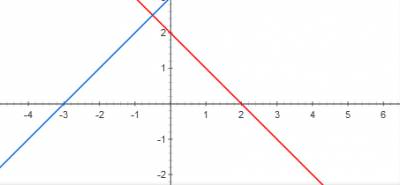
1 mod de a rezolva simplu, găsi un punct de intersecție a graficului:

Coordonata Y a modulului are un triunghi înălțime.

Vom găsi intersecția liniilor drepte cu axa OX, în loc de y pentru a substitui 0 în fiecare ecuație:

lungimea bazei este suma x coordonata intersecție cu modulo plane OX luate:

Conform formulei, cunoscând înălțimea bazei triunghiului și pentru a găsi zona sa:

2 proces, constatarea formulei Teorema fundamentală:

Formula este următoarea:

Citește-l ca o parte integrantă a unui la b, o

Pentru a rezolva o integrală definită, trebuie să găsim mai întâi o funcție primitivă F (X) pentru funcția f (x). Și apoi găsi diferența dintre valorile a și b în primitivă F substituită (x).

Acum, înapoi la exemplul nostru, prima notă de faptul că zona noastră a regiunii este posibil să se calculeze suma a două integralele definite: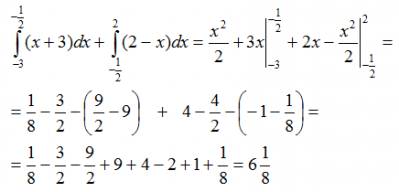

După cum puteți vedea prima metodă este mai ușor de rezolvat, cu toate acestea, nu este întotdeauna posibil să-l folosească, pentru că în afară de calea cea dreaptă poate fi linii curbe. Să le examinăm în exemplul următor.

? 200 '200px': '' + (this.scrollHeight + 5) + 'px'); „> Se calculează aria figurii delimitată de liniile y = x ^ 2-2x + 2, y = x, y = 2x-1

Înainte de a începe să se vedea integrantă clar liniile care au diagrama:

y = x²-2x + 2 - parabole de forma y = ax² + bx + c, ramură direcționată în sus, minciunile apexului la punctul cu coordonate x = -b / 2a, x = 2/2 = 1, y = 1. A (1,1)

y = x și y = 2x-1, se intersectează în punctul A (1,1)

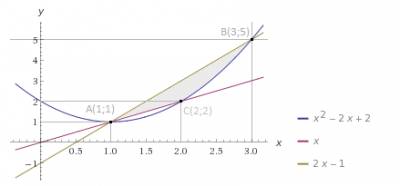
(În imagine este selectată zona dorită, punctul de intersecție specificate Program)

Pentru a găsi o anumită zonă a spațiului necesar figura 1, figura 2 ia o zonă și zona din figura 3, figura 3 se obține din diferența dintre zona zona 4 și figura 5.

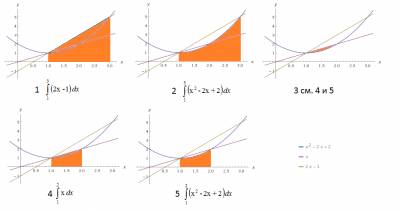
Figura prezintă integralele definite de calcul, pentru fiecare primitivă găsi și înlocui primul punct superior, apoi le scade din partea de jos.

3) (3/2) - (4/3) = (9-8) / 6 = 1/6

forme pătrate selectate în prima imagine este:

10 - (14/3) - (1/6) = (60-28-1) / 6 = 31/6

? 200 '200px': '' + (this.scrollHeight + 5) + 'px'); „> y = 1/3 ^ 3, y = 3

Pentru a rezolva aceste probleme, este foarte important să fie în măsură să exploreze funcția și de a construi programe de rapid, cel puțin schematic.

Începem cu o primă funcție y = (1/3) * x 3

Având în gradul al treilea a spus că este un grafic al parabolei Cubic, și este o curbă elicoidală care trece prin originea primul și al treilea trimestru.

Astfel, la fel ca în x = 0, y = 0 grafic trece prin centrul de coordonate.

Cifra este următoarea:

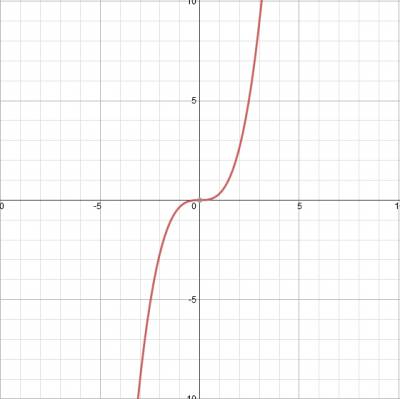
Acum, a doua funcție y = 3, de asemenea, trece prin origine și o linie dreaptă.

Comparabil cu grafic cele două funcții pentru a vedea zona dorită:

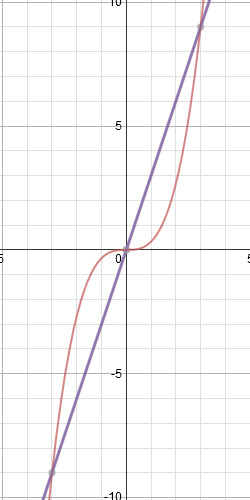
După cum putem vedea, pentru a obține două figuri simetrice, unul în primul și unul în al treilea trimestru.

Pentru a găsi suprafața totală este suficientă pentru a găsi unul dintre ele și se înmulțește cu doi.

Găsim intersecția graficelor de funcții, este suficient pentru a echivala cele două funcții (1/3) * x 3 = 3x:

1 punct (0, 0), punctul 2 (3, 9)

Zona figurii delimitate de curbele y = f1 (x) și y = f2 (x) [f1 (x) ≤ f2 (x)] și direct x = a, x = b este calculat folosind formula y = f1 (x) și y = f2 (x) [f1 (x) ≤ f2 (x)] și direct x = a, x = b se calculează cu formula:

În cazul nostru, ia forma:

Rămâne de a găsi un primitiv:

Apoi aplicați formula Newton-Leibniz pentru integrala definită:

S = F (b) - F (a) = F (3) - F (0)

Apoi, în zona de la 0 la 3 în grafic este egal cu 27/4

Zona completă a figurii delimitată de liniile este 27/2