Valori admisibile DOMENIUL


Site-ul Matematician Feldman Inna Vladimirovna. Servicii profesionale tutore în matematică de la Moscova. Pregătirea pentru DPA și examen, ajuta la cele rămase în urmă.
Intervalul valorilor admise ale expresiilor algebrice (prescurtat TCC) - un set de valori ale unei variabile, în care este definit această expresie.
În cursul algebra școlar are cinci funcții de bază. care au limitat domeniu. Iată-le:
Expresia sub semnul rădăcinii chiar și multiplicitate, trebuie să fie mai mare sau egală cu zero.
Expresia la numitor nu poate fi zero.
Expresia sub semnul logaritmului trebuie să fie strict mai mare decât zero; expresia pe baza logaritmului trebuie să fie strict mai mare decât zero și diferite de unitate.
5.Est două funcții care conțin fracții „ascunse“:
Amploarea rădăcină - un număr natural diferit de 1.
Astfel, funcțiile și au alt domeniu.
În cazul în care expresia conține una sau mai multe funcții care sunt definite pe un set limitat de valori ale argumentului, în scopul de a găsi expresia DHS, este necesar să se ia în considerare toate restricțiile impuse de aceste funcții.
Pentru a găsi o serie de valori admise de expresii, este necesar să se examineze dacă, în ceea ce privește funcția sunt prezente, pe care le-am enumerat mai sus. Și în ceea ce privește detectarea acestor funcții, limitări de înregistrare le-a cerut, trecând de la „exterior“, „interior“.
Permiteți-mi să explic cu un exemplu:
Găsiți domeniul funcției:
Pentru a găsi domeniul funcției. pentru a găsi intervalul de valori admise ale expresiilor. care se află pe partea dreaptă a ecuației funcțiilor
Am ales în mod specific o „teribil“, la prima vedere, funcționează pentru a vă arăta ceea ce o simplă operație este rupt găsi procesul de intervalul de toleranță.
„Crawl de“ expresia de pe partea dreaptă:
1. Vedem o lovitură:
Numitorul nu este zero. scrie:
2. Ne vedem în numitorul logaritmului:
Expresia sub semnul logaritmului trebuie să fie strict mai mare decât zero; expresia pe baza logaritmului trebuie să fie strict mai mare decât zero și diferite de unitate.
3. Am găsit rădăcina pătrată:
Expresia sub semnul rădăcinii chiar și multiplicitate, trebuie să fie mai mare sau egală cu zero.
Acum scrie toate constrângerile din sistemul inegalităților:
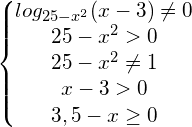
Soluția acestui sistem de inegalități se uite la VIDEUROKE: